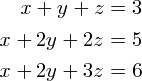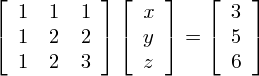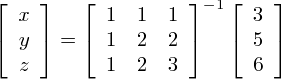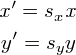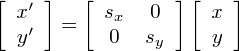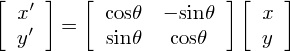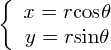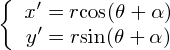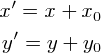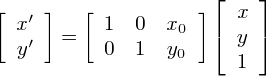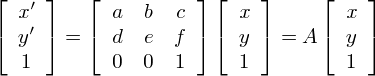OpenCV - 数学演算

ここでは，画像処理に必要な線形代数および統計処理に関する内容を載せていきます.

行列演算 (Matrix operation)
幾何学変換 (Geometric Transform)
統計 (Statistics)
- 最小・最大値
- 平均・標準偏差

行列演算 (Matrix operation)

行列演算(Matrix operation)は画像処理と密接な関係があります.
ここでは行列演算を行う関数を使うために連立方程式を解くプログラムを作成します.

以下の連立方程式を解きます．

行列の形に置き換えると，

この式の両辺に逆行列を掛けると，

上式から，連立方程式の解は係数行列の逆行列を両辺に掛けることで求められます．

係数行列をA，未知の行列をX，右辺の行列をBとします.
X = A-1B

CvMat構造体

行列を定義する
OpenCVで行列を扱うには''CvMat''構造体を利用します．

typedef struct CvMat {
  int type; /* CvMat シグネチャ (CV_MAT_MAGIC_VAL)．要素の型とフラグ */
  int step; /* 全行のバイト長 */

  int* refcount; /* 内部的に利用されるデータ参照カウンタ */

  union {
    uchar* ptr;
    short* s;
    int* i;
    float* fl;
    double* db;
  } data; /* データポインタ */

  #ifdef __cplusplus
  union {
    int rows;
    int height;
  };

  union {
    int cols;
    int width;
  };
  #else
    int rows; /* 行の数 */
    int cols; /* 列の数 */
  #endif

} CvMat;

行列ヘッダの初期化する
行列ヘッダの初期化には''cvMat()''を使います.

CvMat cvMat(int rows, int cols, int type, void* data=NULL);

rows 
   行列の行数.
cols
   行列の列数.
type
   要素の型.
data
   行列ヘッダで指定されるデータへのポインタ.

行列の生成

行列の生成には''cvCreateMat()''を使います.

CvMat* cvCreateMat(int rows, int cols, int type);

rows
   行列の行数．
cols
   行列の列数．
type
   要素の型．CV_32FC1，CV_64FC2など．

例えば，3行3列，各要素が32ビット浮動小数点型 1チャンネルのmatという行列を定義するには以下のように記述します．

この関数は新たな行列とその内部データのためのヘッダを確保し，作成された行列へのポインタを返します.

行列要素に値を代入する
''cvmSet()''を用いて，行列の要素に値を代入します．
(行と列の範囲チェックはデバッグモードの時しか行いません)

void cvmSet(CvMat* mat, int row, int col, double value);

mat
   行列の名前
row
   代入する行番号
col
   代入する列番号
value
   代入する値

行列要素の値を取得する
''cvmGet()''を用いて，行列の要素の値を取得します.
(行と列の範囲チェックはデバッグモードの時しか行いません)

double cvmGet(const CvMat* mat, int row, int col)

mat
   行列の名前．
row
   行番号．
col
   列番号．

ポインタを利用して要素に直接アクセスする.
関数を使わず要素に直接アクセスして値を代入・取得することもできます. // CV_32FC1の場合 ((float*)(matA->data.ptr + matA->step*row))[col] // CV_64FC1の場合 ((double*)(matA->data.ptr + matA->step*row))[col]

行列演算

行列の定義，および行列の各要素に値を代入し，行列演算を行う準備ができました．
以下に基本的な行列演算を行うための関数を示します．

X = A ＋ B	cvmAdd(matA, matB, matX)
X = A - B	cvmSub(matA, matB, matX)
X = AB	cvmMul(matA, matB, matX)
X = A-1 (逆行列)	cvmInvert(matA, matX)
X = AT (転置行列)	cvmTranspose(matA, matX)
X = A・B (内積)	cvmDotProduct(matA, matB)
X = A × B (外積)	cvmCrossProduct(matA, matB, matX)
\|A\| (行列式)	cvmDet(matA)

行列の乗算は cvmMul(), 行列の要素同士のかけ算は cvMul() なので注意.

線形問題または最小二乗法問題を解く
連立方程式を解く場合，''cvSolve()''を利用して解くこともできます.

int cvSolve( const CvArr* A, const CvArr* B, CvArr* X, int method=CV_LU );

A
   入力行列． 
B
   線形システムの右辺． 
X
   出力解． 
method
   逆行列の解法．
   CV_LU - 最適なピボット選択によるガウスの消去法
   CV_SVD - 特異値分解
   CV_SVD_SYM - 対称正定値行列のための特異値分解．

連立方程式を解く #include<stdio.h> #include<cv.h> int main(int argc, char **argv) { // 行列の要素 float dataA[] = {1.0, 1.0, 1.0, 1.0, 2.0, 2.0, 1.0, 2.0, 3.0}; float dataB[] = {3.0, 5.0, 6.0}; // 行列を生成する CvMat matA = cvMat(3, 3, CV_32FC1, dataA); CvMat *matAinv = cvCreateMat(3, 3, CV_32FC1); CvMat matB = cvMat(3, 1, CV_32FC1, dataB); CvMat *matX = cvCreateMat(3, 1, CV_32FC1); // 行列演算を行う cvmInvert(&matA, matAinv); cvmMul(matAinv, &matB, matX); // or cvMatMull() /* cvSolve(&matA, &matB, matX, CV_LU); cvSolve()関数を利用してもよい */ for(int row=0; row<matX->rows; row++){ for(int col=0; col<matX->cols; col++){ printf("%.1f ", cvmGet(matX, row, col)); } printf("\n"); } // 行列のメモリを解放する cvReleaseMat(&matAinv); cvReleaseMat(&matX); return 0; } 出力結果：
```
1.0  //x
1.0  //y
1.0  //z
```

幾何学変換 (Geometric Transform)

画像の幾何学変換(Geometric Transform)とは，画像に対して幾何学的な変化を加える処理です．
これは，拡大縮小や回転などを用いて画像を変形する処理を意味します．

幾何学変換は画素の座標(x,y)を他の座標(x',y')に移動させることによって行われ，移動先の座標(x',y')は元の座標(x,y)に変換行列Aを掛け合わせることによって求められます．

拡大・縮小

画像をx軸方向にsx倍，y軸方向にsy倍する処理を考えます．

これを行列の形で書き表すと，

となります．この右辺左側の行列が，拡大縮小を行う変換行列となります．

OpenCVでは，画像の拡大縮小を''cvResize()''で行います．

void cvResize(const CvArr* src, CvArr* dst, int interpolation=CV_INTER_LINEAR);

src
   入力画像． 
dst
   出力画像． 
interpolation
   補間方法．

   * CV_INTER_NN - ニアレストネイバー法
   * CV_INTER_LINEAR - バイリニア補間 (デフォルト)
   * CV_INTER_AREA - ピクセル領域の関係を用いてリサンプリングする．
                     画像縮小の際は，モアレの無い処理結果を得ることができる．
                     拡大の際は，CV_INTER_NN と同様
   * CV_INTER_CUBIC - バイキュービック補間

出力画像dstのサイズに合わせて入力画像srcを拡大あるいは縮小し，変換結果をdstに格納します．

補間方法について
幾何学変換では理論上は変換行列を用いることで実現できますが，デジタル画像においては，入力画像の各座標値に変換行列を掛け合わせただけでは不完全です．それはデジタル画像の座標は正の整数値で表現されるため，小数点を含んだ座標を参照することが出来ないからです．そこで，小数点を含む座標における画素値を計算するために様々な画像補間法が提案されています．
- ニアレストネイバー法
  補間される画素の座標が小数点を含む場合，最も近い座標を選ぶ手法．
  エッジは保存されますが，拡大したときに粗さが目立ちます．
- バイリニア補間
  補間される座標の近傍4画素の値を用いて1次補間を行って画素の値を決める手法．
  最近隣接補間と比べて滑らかな補間結果が得られます．
- バイキュービック補間
  補間される座標の近傍16画素の値を用いて3次補間を行って画素の値を決める手法．
  最も粗さの少ない画像が得られますが，エッジなどがぼやける傾向にあります．

グラデーションを反映させたいのであればバイキュービック補間，エッジのはっきりした画像を作りたいのであれば最近隣接補間を用います．また，バイリニア補間はその中間の性質を持ちます．

回転

画像を水平からy軸正方向にθだけ回転させる処理を考えます．
回転行列は以下のようになります．

''導出''
回転行列さえ知っていればいいので，ここは知りたい人だけ見てくれればいいです．
ここでは高校数学(数II)程度の知識が必要です.

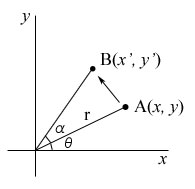
座標A(x,y)から座標B(x',y')にαだけ回転する場合．

A，Bはそれぞれは以下の式で表されます．

Bのx'は加法定理より，

となり，Aの式より，

となります．同様にy'についても，

となり，回転行列(変換行列)は前述のようになります．

画像を回転させるには，まず回転行列(変換行列)を求め，その後で入力画像に掛け合わせます．
回転行列を求めるには''cv2DRotationMatrix()''を用います．

CvMat* cv2DRotationMatrix(CvPoint2D32f center, double angle,
                          double scale, CvMat* map_matrix);

center
   入力画像内の回転中心．
angle
   反時計方向を正とする回転角度． 
scale
   スケーリング係数（x,y方向とも同じ係数 scale を使う） 
map_matrix
   2×3 変換行列．

CvPoint2D32fはCvPointのxおよびyの型がfloat型の構造体です．
また，画像の拡大縮小を同時に行いたい場合はscaleに指定します．
(ただし，画像の縦横比を変更することは出来ません．)
CvMat構造体については前節を参照してください．
求められた回転行列はmatrixに格納されます．

cv2DRotationMatrix()で求めた回転行列を画像に適用し回転させます．
この回転行列を適用するには''cvWarpAffine()''を用います．

void cvWarpAffine(const CvArr* src, CvArr* dst, const CvMat* map_matrix,
                  int flags=CV_INTER_LINEAR+CV_WARP_FILL_OUTLIERS,
                  CvScalar fillval=cvScalarAll(0));

src
   入力画像． 
dst
   出力画像． 
map_matrix
   2×3 変換行列． 
flags
   補間方法（CvResizeを参照）と，以下に示すオプションフラグの組み合わせ．

   * CV_WARP_FILL_OUTLIERS - 出力画像の全ピクセルの値を埋める．
                             対応の取れないピクセルは，fillvalがセットされる．
   * CV_WARP_INVERSE_MAP - 出力画像の座標値を元に，対応する入力画像の座標を求める逆変換を行う．

fillval
   対応の取れない点に対して与える値．

CvScalar構造体
fillvalの型になっているCvScalar構造体はOpenCVの多くの関数で引数に取るのでぜひ覚えておきましょう．
中身は4個までの値を納めるdouble型の配列です．

typedef struct CvScalar {
  double val[4];
} CvScalar;

/* コンストラクタ：val[0] を val0 で初期化．val[1] を val1 で初期化．… */
inline CvScalar cvScalar(double val0, double val1=0, double val2=0, double val3=0);
/* コンストラクタ：val[0]...val[3] を val0123 で初期化 */
inline CvScalar cvScalarAll(double val0123);
/* コンストラクタ：val[0] を val0 で初期化．val[1]...val[3] を 0 で初期化 */
inline CvScalar cvRealScalar(double val0);

平行移動

画像を(x0,y0)だけ平行移動させる処理を考えます．

これを行列で表すと，

画像を平行移動させるために変換行列を求めます．
変換行列を求めるには''cvGetAffineTransform()''を用います．

CvMat* cvGetAffineTransform(const CvPoint2D32f* src, const CvPoint2D32f* dst, 
                            CvMat* map_matrix);

src
   入力（変換前）画像内に存在する三角形の3つの頂点座標． 
dst
   出力（変換後）画像内に存在するsrcに対応した三角形の3つの頂点座標． 
map_matrix
   2×3 変換行列．

src，dstには3つの座標が一直線に並ばないように値を選ぶ必要があります．

変換行列が求められたら，回転の時と同様にcvWarpAffine()を用いて画像の平行移動を行います．

アフィン変換 (Affine Transform)

ここまで画像の拡大縮小，回転，平行移動を扱ってきました．
これらの変換行列は以下のように一般化されています．

a~fはそれぞれ任意の実数です．

このような3行3列の変換行列による2次元画像の幾何学変換を''アフィン変換(Affine Transform)''といいます．
拡大縮小，回転，平行移動はアフィン変換の一種です．
このアフィン変換行列Aのパラメータを変化させることで，より複雑な形への幾何学変換が可能です．

画像をアフィン変換により変形する #include <stdio.h> #include <cv.h> #include <cxcore.h> #include <highgui.h> int main(int argc, char **argv) { // lena.jpgを読み込む 256x256[pixel] IplImage *srcImg = cvLoadImage("lena.jpg", CV_LOAD_IMAGE_ANYDEPTH | CV_LOAD_IMAGE_ANYCOLOR); if(srcImg == NULL){ printf("Can't Load Image.\n"); return -1; } IplImage *dstImg = cvCreateImage(cvGetSize(srcImg), IPL_DEPTH_8U, 3); // 変換前座標 3点 CvPoint2D32f original[] = {cvPoint2D32f(0, 0), cvPoint2D32f(srcImg->width, 0), cvPoint2D32f(0, srcImg->height)}; // 変換後座標 3点 CvPoint2D32f translate[] = {cvPoint2D32f(80, 80), cvPoint2D32f(230, 30), cvPoint2D32f(30, 230)}; CvMat *affineMatrix = cvCreateMat(2, 3, CV_32FC1); // 変換行列を求める cvGetAffineTransform(original, translate, affineMatrix); // 変換行列を適用する(アフィン変換) cvWarpAffine(srcImg, dstImg, affineMatrix, CV_INTER_LINEAR | CV_WARP_FILL_OUTLIERS, cvScalarAll(0)); cvNamedWindow("変換前", CV_WINDOW_AUTOSIZE); cvNamedWindow("変換後", CV_WINDOW_AUTOSIZE); cvShowImage("変換前", srcImg); cvShowImage("変換後", dstImg); cvWaitKey(0); cvReleaseImage(&srcImg); cvReleaseImage(&dstImg); cvDestroyAllWindows(); return 0; }

統計 (Statistics)

ここで紹介する関数は自前で書いてもそれほど手間はかかりませんが，OpenCVに用意されている関数を利用すると便利です．
基本的にはすべて配列操作の関数です.

最小・最大値

配列内要素の最小・最大値およびその位置を求めるには''cvMinMaxLoc()''を用います．

void cvMinMaxLoc(const CvArr* arr, double* min_val, double* max_val,
                 CvPoint* min_loc=NULL, CvPoint* max_loc=NULL, const CvArr* mask=NULL);

arr
   入力配列（シングルチャンネルまたはCOIがセットされたマルチチャンネル）． 
min_val
   戻り値の最小値へのポインタ． 
max_val
   戻り値の最大値へのポインタ． 
min_loc
   戻り値の最小値を持つ位置へのポインタ． 
max_loc
   戻り値の最大値を持つ位置へのポインタ． 
mask
   部分配列を指定するためのオプションのマスク．

画素値の最小・最大値およびその座標位置を求める #include <stdio.h> #include <cv.h> #include <highgui.h> int main(int argc, char **argv){ IplImage *img = 0; double minVal = 0.0, maxVal = 0.0; CvPoint minLoc = cvPoint(0,0); CvPoint maxLoc = cvPoint(0,0); if((img = cvLoadImage("lena.jpg", CV_LOAD_IMAGE_GRAYSCALE)) == 0) return -1; printf("Calculate the Min/Max and Location.\n"); cvMinMaxLoc(img, &minVal, &maxVal, &minLoc, &maxLoc); printf("Min = %f, Loc(x, y) = (%d, %d)\n", minVal, minLoc.x, minLoc.y); printf("Max = %f, Loc(x, y) = (%d, %d)\n", maxVal, maxLoc.x, maxLoc.y); cvReleaseImage(&img); return 0; } 出力結果:
```
Calculate the Min/Max and Location.
Min = 18.000000, Loc(x, y) = (265, 198)
Max = 248.000000, Loc(x, y) = (116, 273)
```

平均・標準偏差

配列内要素の平均・標準偏差を求めるには''cvAvgSdv()''を用います．

void cvAvgSdv(const CvArr* arr, CvScalar* mean, CvScalar* std_dev, const CvArr* mask=NULL);

arr
   配列． 
mean
   計算結果の平均値へのポインタ．必要でない場合は NULL． 
std_dev
   計算結果の標準偏差へのポインタ． 
mask
   オプションの処理マスク．

関数 cvAvgSdv() は，配列要素の平均と標準偏差を各チャンネルで独立に計算します．

画像の各チャンネルの平均および標準偏差を求める #include <stdio.h> #include <cv.h> #include <highgui.h> int main(int argc, char **argv){ IplImage *img = 0; CvScalar mean = cvScalarAll(0); CvScalar std_dev= cvScalarAll(0); if((img = cvLoadImage("lena.jpg", CV_LOAD_IMAGE_ANYDEPTH | CV_LOAD_IMAGE_ANYCOLOR)) == 0) return -1; printf("Calculate the Mean and Standard-Deviation.\n"); cvAvgSdv(img , &mean, &std_dev); printf("Mean(B,G,R) = (%f, %f, %f)\n", mean.val[0], mean.val[1], mean.val[2]); printf("Standard-Deviation(B,G,R) = (%f, %f, %f)\n", std_dev.val[0], std_dev.val[1], std_dev.val[2]); cvReleaseImage(&img); return 0; } 出力結果：
```
Calculate the Mean and Standard-Deviation.
Mean(B,G,R) = (105.398991, 99.562698, 179.730305)
Standard-Deviation(B,G,R) = (33.742055, 52.873458, 49.015695)
```